The term crop factor refers to the ratio of a specific sensor to a 35mm full-frame sensor. This factor determines the equivalent field of view of a lens when used on a camera with a sensor that is either smaller or larger than our reference full-frame sensor.
Many people are familiar with the two common APS-C crop factors: 1.6x for Canon, and 1.5x for Nikon, Fuji, Sony, etc. But how do we get to this number, and how do you calculate the crop factor for other sensor sizes?

Table of Contents
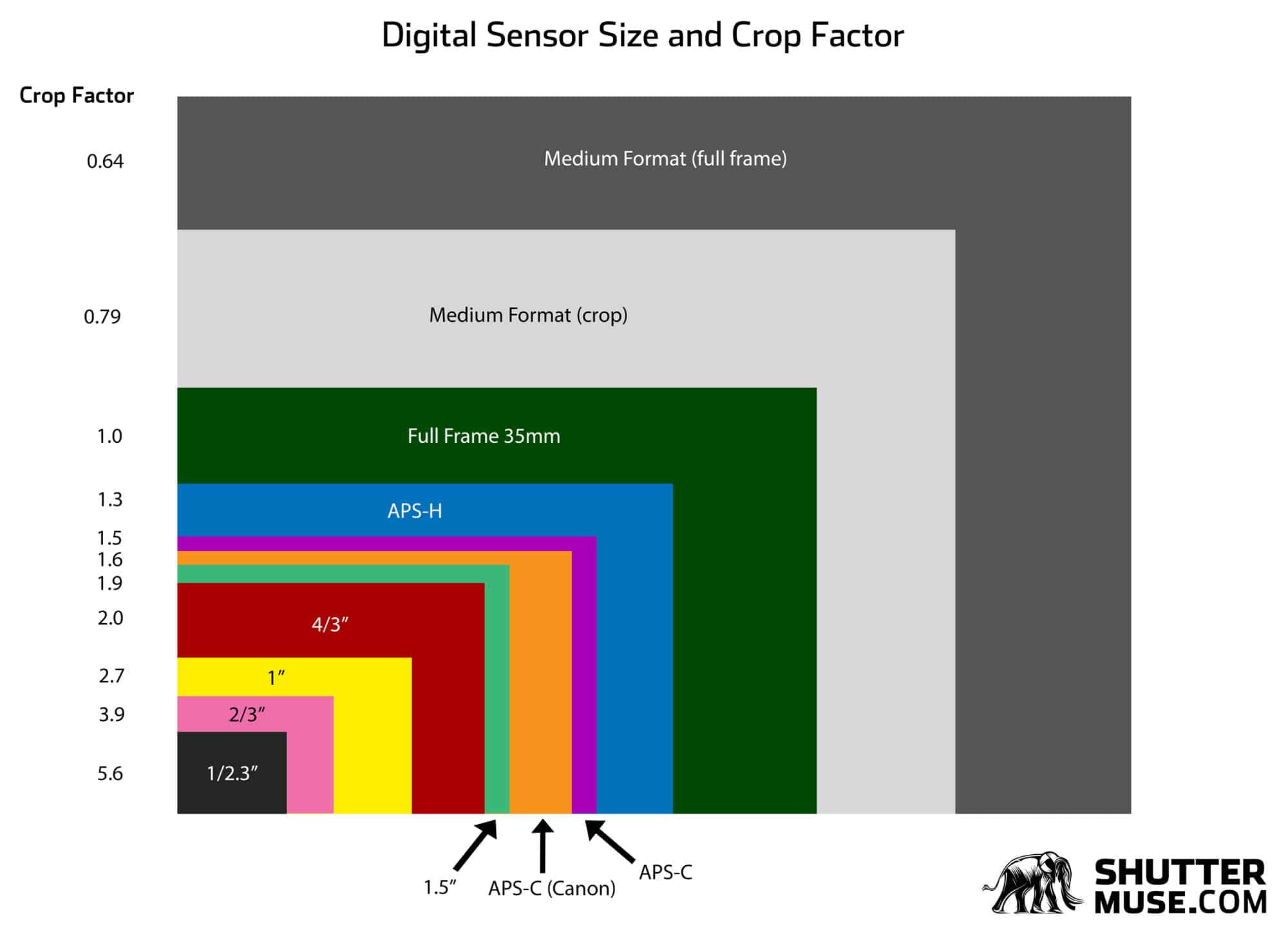
Digital Sensor Sizes and Their Crop Factor
These are the most common crop factors for modern digital camera sensors. In the next section I will show you how we calculated these figures, and how you can apply them to any digital sensor to work out its crop factor, and the resulting field of view of a lens.
Camera Crop Factor Table
| Sensor Size | Sensor Dimensions | Crop Factor |
|---|---|---|
| Medium Format | 53.7mm x 40.4mm | 0.64 |
| Medium Format – cropped (eg. Fuji GFX) | 43.8mm x 32.9mm | 0.79 |
| Full Frame 35mm | 36mm x 24mm | 1 |
| APS-H | 27.9mm x 18.6mm | 1.3 |
| APS-C | 23.6mm x 15.6mm | 1.5 |
| APS-C (Canon) | 22.2mm x 14.8mm | 1.6 |
| 1.5″ | 18.7mm x 14mm | 1.9 |
| 4/3″ | 17.3mm x 13mm | 2 |
| 1″ | 12.8mm x 9.6mm | 2.7 |
| 2/3″ | 8.8mm x 6.6mm | 3.9 |
| 1/2.3″ | 6.17mm x 4.55mm | 5.6 |
How to Calculate Crop Factor
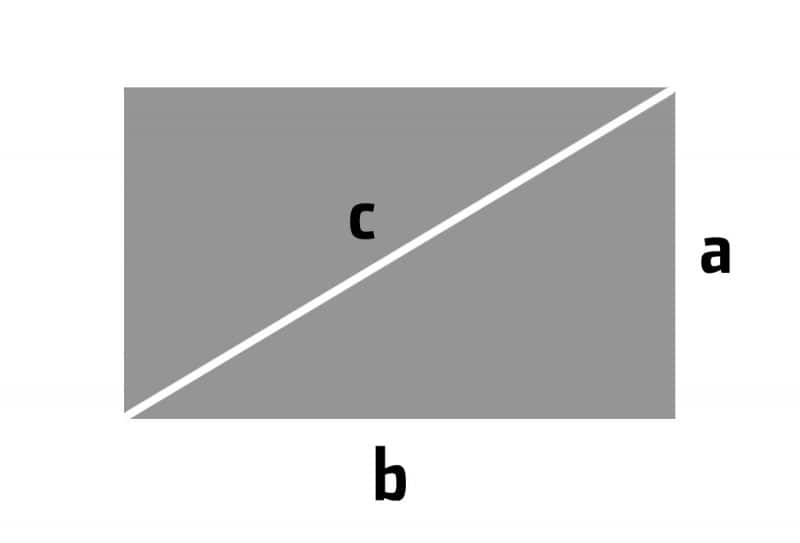
The critical thing to know is that the crop factor is the ratio of the diagonal dimension of the sensor. Manufacturers often provide the horizontal and vertical dimensions, so we can use Pythagorean theory to calculate the diagonal measurement.
c2 = a2 + b2
therefore
c = √(a2 + b2)
Full frame sensor dimensions: 36 mm x 24 mm therefore diagonal dimension is √(362 + 242) = 43.27 mm
Crop Factor Calculation Example
Our reference is always a 35mm full-frame sensor. In the previous section, we calculated its diagonal dimension as 43.27mm. Now we need to calculate the diagonal size of the sensor for which you are trying to find the crop factor.
Canon APS-C Crop Factor Calculation
We’ll work with a Canon APS-C sensor with 22.2 x 14.8 mm dimensions for our first example.
Let’s go through it step by step:
- Full-frame sensor diagonal dimension: 43.27 mm
- Canon APS-C dimensions: 22.2 x 14.8 mm
- Therefore Canon APS-C diagonal dimension is √(22.22 + 14.82) = 26.68 mm
- Therefore crop factor equals: 43.27/26.68 = 1.621814 -> rounded to 1.6 for general usage
Nikon, Sony and Fujifilm APS-C Crop Factor
All of Fujifilm’s X Series cameras use an APS-C sensor with dimensions of 23.6 mm x 15.6 mm. Sony and Nikon’s APS-C cameras also use sensors with the same dimensions.
- Full frame sensor diagonal dimension: 43.27 mm
- Fuji, Sony and Nikon APS-C dimensions: 23.6 x 15.6 mm
- Therefore their APS-C diagonal dimension is √(23.62 + 15.62) = 28.29 mm
- Therefore crop factor equals: 43.27/28.29 = 1.515729 -> rounded to 1.5 for general usage
Applying Crop Factor to Find Equivalent Field of View

We want to know the crop factor of a camera to understand what kind of field of view we will get with a particular focal length. For example, placing a 50mm lens on an APS-C camera will give us a field of view equivalent to a much longer lens on a full-frame camera. For a Canon APS-C camera, that would be 1.6×50 = 80mm.
In other words, a 50mm lens on an APS-C camera delivers the same field of view as an 80mm lens on a full-frame camera. If you wanted that “normal” 50mm framing on an APS-C camera, you would reverse the process and divide 50/1.6, giving you 31.25mm. This means that you could use a lens that covered that focal length, perhaps a 24-70mm zoom, and set it to about 32mm to replicate the field of view of a standard 50mm lens if you were using an APS-C camera instead of a full-frame camera.






fantastic for curious people who wants to know facts.
Thanks!
Hello Dan,
The Think Tank free gifts with an order of 50$ or more is it available for a customer with a shipping address in Canada ?
Thank you for the follow-up.
Jean
Unfortunately I don’t think they ship internationally from their website.
Thank you, I was able to use this to correct someone who was wrongfully claiming the BMPCC 4K is 1.9x crop (they were dividing sensor width by height. Sigh he had the gall to say I was wrong the BMPCC 4K’s crop factor was 2.0, which I was able to verify with the above calculations.
Glad it helped!
Thank you for this article. I’m a bit confused. On their website, they say that their sensor size is 18.96mm x 10mm (Four Thirds). I see two different versions of 4/3 conversions. Could you help me understand? Here’s the info page: https://www.blackmagicdesign.com/products/blackmagicpocketcinemacamera/techspecs/W-CIN-12
I’m trying to choose between two Canon cameras for my EF zoom lenses.
One is 24mp APSC (M50 II), and the other a 50mp FF (5DS R) , which is older, larger, and twice the price. If I will be cropping the FF images severely (for small birds), would it be better to purchase the APS C for pixels and for image quality?