The Fujifilm GFX mirrorless medium format system has gone from strength to strength in recent years. What was once a limited lens selection has now been filled out with focal lengths from 23mm up to 500mm, with few gaps along the way. What’s more, there are now specialist lenses in the Fuji GF lens lineup, such as the GF 120mm macro, the GF 30mm f/5.6 Tilt-Shift lens, the GF 500mm f/5.6, and the stunning GF 80mm f/1.7.
The launch of the original 50MP GFX 50S was a revolution in the industry. Never had there been a more affordable way to get into digital medium format photography. While Pentax did pave the way with the 645Z, Fujifilm undercut the price significantly while offering a more modern set of features. After that, we saw the even cheaper GFX 50R rangefinder-style camera, the ground-breaking GFX 100, and then the GFX 100s and GFX 100 II. Incredibly, after just a few short years from launch, we are at a place where you can get a 100MP medium format camera with image stabilization for just $4999, and it’s no bigger than a DSLR.
It’s clear that DSLRs are well on their way to being extinct, and it honestly looks like some companies such as Nikon and Panasonic might have made too many missteps in their transition to a mirrorless world. I worry for their future. But Fujifilm has always walked its own path. By carving out their own unique corner of the market with the GFX system, I’m sure they have a bright future.
Calculating 35mm Equivalent Focal Lengths for Fujifilm GF Lenses
Most people are used to seeing lens focal lengths quoted in 35mm terms. With the GFX system using a much larger sensor than that in a full-frame camera, lens focal lengths are not equivalent. In other words, a 50mm lens on a full-frame camera will have a completely different field of view to a 50mm lens on the GFX system. This makes it tricky to see focal lengths for the Fujifilm GF lenses and immediately comprehend how wide or tight their field of view is.
Thankfully, it’s relatively easy to convert the focal length of a Fujifilm GF lens into a 35mm equivalent that is usually easier to visualize if you’re considering a move from a full-frame mirrorless system to the GFX system. To perform the focal length equivalence conversion, we first need to figure out the crop factor of the GFX sensors compared to a full-frame 35mm sensor.
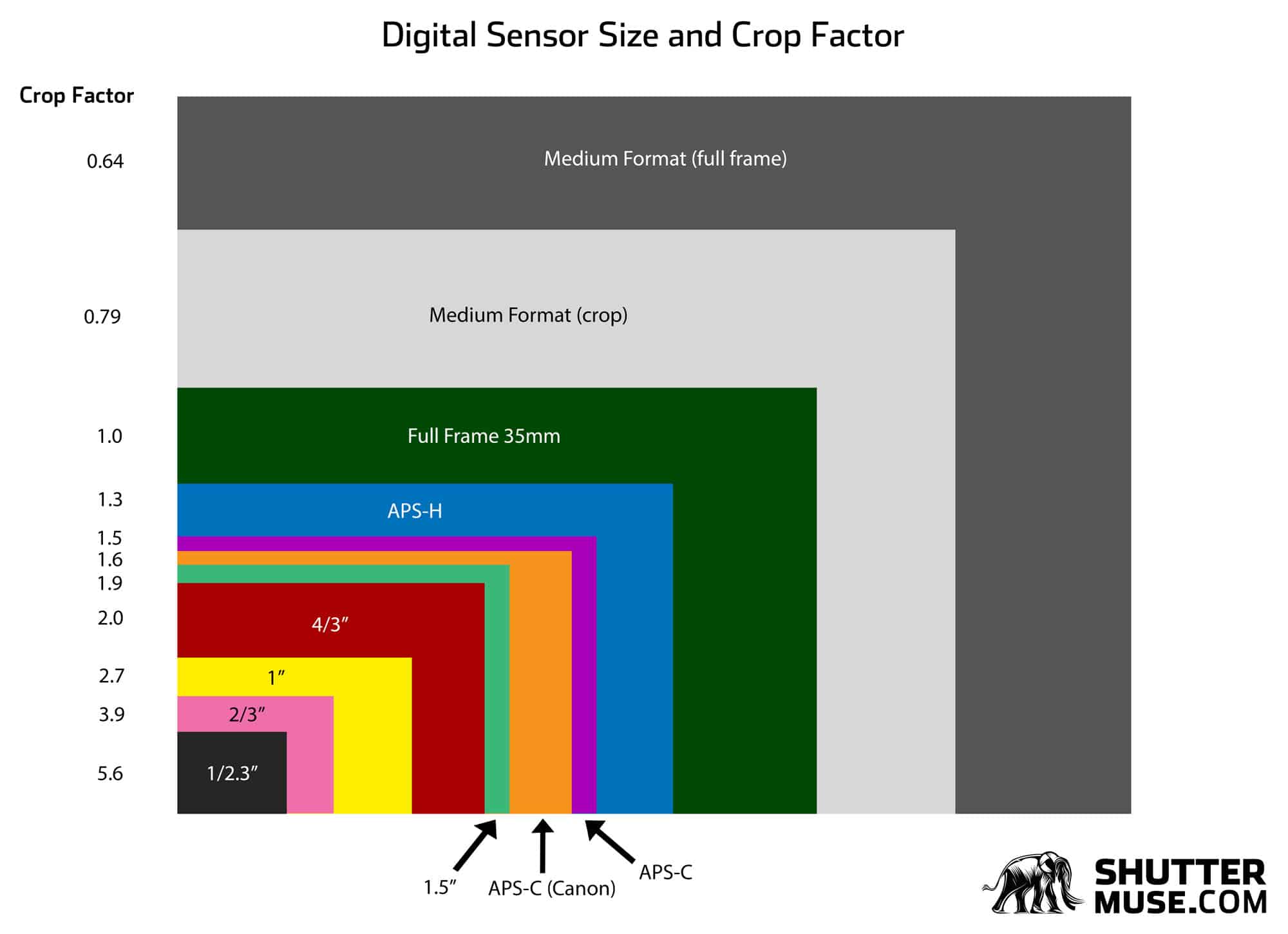
Crop Factor for Fujifilm GFX System Cameras
Crop factor is the ratio of the diagonal dimension of two camera’s sensors. If you know the width and height of a sensor, you can calculate the diagonal dimension using Pythagorean theory. Then you simply divide the diagonal dimension of a full-frame sensor, by the diagonal dimension of the sensor for which you want to find the crop factor. The Fujifilm GFX system in our case.
Most of us are used to seeing crop factor represented as a number greater than 1. For example, APS-C cameras typically have a crop factor of 1.5x or 1.6x. Since the GFX system has a sensor that is larger than full-frame, we can expect our crop factor to be less than 1. In other words, 35mm full-frame equivalent focal lengths will be wider than the quoted focal length for any given GF lens.
The math works out as follows:
Full frame sensor dimensions: 36mm x 24mm therefore diagonal dimension is √(362 + 242) = 43.27mm
GFX format sensor size: 43.8mm x 32.9mm therefore diagonal dimension is √(43.82 + 32.92) = 54.78mm
Crop factor for Fujifilm GFX system = 43.27/54.78 = 0.79
Fuji GF Lens Equivalent Field Of View Table
Using the calculated crop factor of 0.79, we can now see the 35mm equivalent field of views for all the Fuji GF lenses. If you want to see more details about the GF lens lineup, I suggested you also take a look at our database of all the specifications for every Fujifilm GF lenses.
| Lens | 35mm Full-Frame Equivalent | Equivalent F-Stop |
|---|---|---|
| GF 23mm f/4 R LM WR | 18mm | f/3.2 |
| GF 30mm f/3.5 R WR | 24mm | f/2.8 |
| GF 30mm f/5.6 T/S | 24mm | f/4.5 |
| GF 32-64mm f/4 R LM WR | 25-51mm | f/3.2 |
| GF 35-70mm f/4.5-5.6 WR | 28-55mm | f/3.5-4.5 |
| GF 45-100mm f/4 R LM OIS WR | 36-79mm | f/3.2 |
| GF 45mm f/2.8 R WR | 35mm | f/2.2 |
| GF 50mm f/3.5 R LM WR | 40mm | f/2.8 |
| GF 55mm f/1.7 R WR | 44mm | f/1.3 |
| GF 63mm f/2.8 R WR | 50mm | f/2.2 |
| GF 80mm f/1.7 R WR | 63mm | f/1.3 |
| GF 100-200mm f/5.6 R LM OIS WR | 79-158mm | f/4.5 |
| GF 110mm f/2 R LM WR | 87mm | f/1.6 |
| GF 110mm f/5.6 T/S Macro | 87mm | f/4.5 |
| GF 120mm f/4 R LM OIS WR Macro | 95mm | f/3.2 |
| GF 250mm f/4 R LM OIS WR | 198mm | f/3.2 |
| GF 250mm f/4 R LM OIS WR + 1.4x extender | 277mm | f/4.5 |
| GF 500mm f/5.6 R LM OIS WR | 395mm | f/4.5 |
| GF 500mm f/5.6 R LM OIS WR + 1.4x extender | 553mm | f/6.3 |










Wait. Wait. Wait. Since medium format predates 35mm film, the 35mm is the CROP SENSOR. So … the 35mm sensor has a crop factor of 54.78/43.27 ~= 1.27 and an APS-C sensor would have a crop factor of approximately 1.9.
Hit the button to quickly.
The GFX is NOT A crop sensor camera. What you are calling crop factor is really a MAGNIFICATION FACTOR.
And “large format” predates medium format, so I guess we’re all full of crops…
LOL!!!
Hi Williams. In the title of the post, it says “35mm full frame equivalent” so it’s implied that this is our baseline. You are splitting hairs here for the sake of argument. I’m not the one inventing this terminology, this stuff is used universally in the photography industry. There has to be some reference point, and in the photo industry we use the 35mm simply because it is these focal lengths that everyone is most familiar with. As Rob pointed out below, large format predates medium format, and if you want to really split hairs, should be be basing our factors on the size of daguerrotype film? No, of course not, because the vast majority of people aren’t familiar with the field of view from such a camera so it would create unnecessarily awkward numbers for people to constantly deal with.
As for calling it crop vs. calling it magnification factor, they are exactly the same thing. The term “crop” is universally accepted in the industry. Compared to what most would term full frame medium format, yes the GFX is a crop sensor. It is smaller than true medium format and therefore that crop creates a magnification factor. Same thing.
Erm no Crop comes from old school dark room practices. Crop meant to reduce the size and Blow up meant to increase. So really its a Blow Camera, which to be honest if you can afford Medium format you can probably afford Blow too 🙂
Cropping and blowing up are in no way each others opposites. Cropping means cutting material off. Blowing up means nothing really but implies projecting the negative image on a large sheet. But what is large? That’s arbitrary. There was no opposite to cropping since there was no way to add information to the sides you’re adding too. Maybe a panorama or some other stitching method would be that. Nowadays you can also use generative fill.
Stop playing with terms one is 54.78mm square and the other is 43.27 end of discussion these terms are not Mathematical and bigger is better! That’s it! Smaller cancer reads faster and you can get a steady shot easier that’s it!
I wonder why ‘full frame’ medium format digital is not equal in size to actual medium format 120/220 film, i.e., 56×41.5mm, 56×56, 56x67mm etc. It would make sense, considering “full frame” small format digital takes its size from the frame size of 35mm film.
To state it more succinctly: Small format digital is based around 35mm film as a sizing standard, but medium format is not based around medium format film. Doesn’t make a lot of sense.
Yeah, I’ve often wondered that myself.
“Medium Format” is anything larger than 35mm but smaller than 4×5. 110/220 is really a format produced for the Brownie No.2, which was an amateur camera. As emulsions improved in the 40’s, 50’s and 60’s 135 and 110/220 overtook the large format press cameras.
Tri-X pushed in 135 was pretty painful, but OK for half tone pictures. But 110/220 was good enough and survived, but it is only a common form of “medium format” and not the definitive size.
Thanks! Great knowledge, Greg!
Has to do with silicon manufacturing yields. Silicon manufacture is not a perfect process. Smaller cuts tend to give higher yields. Full sized medium format is not yet cost effective in this age but crop medium format already is.
Same reason why aps-c digital cameras came to market first before full frame 35mm.
No other reason but that.
Good knowledge! Thanks for sharing.
I wonder in time if Fujifilm will regret designing lenses for the cropped MF format, though? If full frame MF becomes financially viable, people will have to buy all new lenses.
Probably not. The practical difference between 35mm FF and “Cropped” Medium format sensors is stunning. Cropped MF sensors have twice the surface area as 35mm, and the resulting output shows. The first time I loooked at a raw file from the Fujfilm 50R I made, I was literally blown away. Sitting there in my chair with my jaw hanging (this is not an exaggeration).
I realized right then that a lot of FF fans were going to be butt hurt when they realized how much better these sensors (and lens combinations) are than full frame.
With the GFX 100S stepping on the toes of FF cameras in size, price, and performance, look out. I think that camera signals the first true MF digital camera to compete with pro level FF systems. I heard Fujifilm preorders of it are THROUGH THE ROOF.
-Carl
(www.photographic-central.blogspot.com)
I agree that the X100S is a huge leap. It feels like Fujifilm have now got to the place that they always intended with that camera.
Because sensors that size would be ridiculously expensive, if they could even produce them in quantities worth manufacturing them. There is a certain amount of rejection/waste calculated into the cost. And… sensors are so good now that we can achieve photo quality equivalents in a smaller chip size. 35mm sensors are approaching or at former medium format film resolution and medium format sensors at 4X5 film resolution. So it’s not really necessary to produce chips that large which would cost enormous amounts of money.
I don’t consider 6 x 4.5 a “full frame medium format”. 6 x 4.5 is in fact only a half frame medium format, like 18 x24mm is 35mm half frame format. To be full frame, a rectangular format must be larger than a square format using the whole width of the film. With 120 film that means 6×7, or even 6×9 if compared to the same aspect ratio of a 24x36mm frame.
indeed medium format is everything larger then 24×36 and smaller then 4×5 inch, the cropfactor range is referenced to the diagonal of 24×36. Even so important is de square usable size of a sensor in relation to the number of pixels. Example 43 sensors used in the olympus and panasonic are 25% of the 24×36 (FF), APS-C is 50% of the area of FF and the 44×33 is 170% against FF. An 43 camera like the olympus with 16MP shall have 32MP on the area of APS-C and 64MP on a FF camera. If we use the same density ore size of the pixels. But we don’t and that means that a APS-C sensor of 16MP has pixels twice the size of an Olympus/Panasonic 43 ore a FF camera with 16MP has 4 times the pixel size of a 43.
What does it mean: Bigger pixels means more catching light, higher contrast and more color information and less need to ultra high resolution lenses.
Everbody can consider what important is for them self
Excellent points! Thanks for joining the conversation, Ricardo!
so actually we get more shallow dof from full frame camera with those very large f stop lens.
If you’re just looking at the apertures, you can’t really tell. The aperture is just a measure of the amount of light that can come in through the lens. You can only compare DoF by looking at aperture if you maintain the same sensor size.
Sensor size is irrelevant to DoF.
DoF is a product of iris opening versus focal range in relation to the distance of a subject.
For practical considerations, it is relevant. On APS-C you would use a 35mm F2 lens where you would use a 50mm F2 on FF. The 35mm lens has more depth of field than the 50mm.QED
Bertrand Yes is Very relevant, try shooting with a GFX kit the shallowness of your DOF is one of the first things you have to adjust to. Higher ISOs and stopping down just to get a decent depth of focus.
WRONG WRONG WRONG….nothing to do with Sensor size just like you can technically match DFO with an APS-C vs a FF provided the APS-C lens is fast enough.
So yes, that 110 F2 lens for example, we can have mode DOF control with a FF with say the Canon 85mm 1.2 or the Sigma 105mm 1.4
A techical fact in every sense but practically speaking in the context of laymen, it does not tell the whole story.
….wow , anyway thanks for the chart, very usefull.
Hi, thanks for all the GOOD info.
Question…
My goal is to make large prints in 35mm print format and slightly thinner and longer prints. I have a Canon 5d/s , 50 Million pixel sensor.
I am looking into moving to Medium format Fuji GFX. Is it worth it to achieve my goal..?
Thanks.
Serge.
With the Fuji, your main advantage is probably going to be the better dynamic range since the pixel count is the same. The sharpness of the images, assuming you are using top end glass on both, would be relatively similar and probably not contribute much to the decision of how large you would print…
So yes, the GFX will give you a better image in terms of dynamic range and tonality, but it doesn’t necessarily mean you could print it much larger as they would be similarly sharp. You might want to look at this incredible software: https://topazlabs.com/gigapixel-ai/ref/54
This software can definitely enable you to make some larger prints and it might be worth trying that first with your 5Ds before investing in an entire new system.
50mp from the canon is more than enough. HOWEVER you have given bad advice here IMHO. A 50MP medium format sensor will ALWAYS out perform a FF 50MP sensor/frame. Pixel to pixel, dynamic range, color, depth, DOF, shadows and highlights, enlargements, etc.
The question was whether the Fuji was worth it to achieve the OPs goal. We both seem to agree that the Canon is more than enough. We also both agree that the image quality from the Fuji would be better, but better dynamic range, for example, doesn’t translate into an ability to create larger prints.
It is possible that FF sensor can beat larger sensors at same megapix counts. Sensor manufacturing abilities and technologies employed can tip the scales.
What’s also interesting to consider, is that Sony is making all these MF sensors anyway. So there is the same technology going into FF and MF sensors.
How long is a piece of string?
How large is large? How far away will they be viewed from? What printer will be used? Do you need to crop? What lenses? Without these pieces of information it is an impossible question.
Undoubtedly a 50 megapixel Canon will be absolutely fine for massive exhibition prints multiple feet across if used correctly.
The GFX has a different aspect ratio so if you are intending to do 3:2 ratio prints you would need to crop pixels to make it narrower and this would probably offset any advantages of the bigger sensor. If you wanted to produce square or 4×5 images it might be different.
The fact that you are asking the question suggests your knowledge/skill doesn’t match your gear. Is the 5D/S not producing prints of high enough quality or have you not even tried yet?
I think this was in reply to serge barbeau. You make some good points RE aspect ratio and cropping. Thanks for joining the conversation Roger.
I was sent this page by someone at Fotodiox trying to work out the equivalent focal length of a lens designed for a 6×7 camera on the GFX. Math is not my strong suit, so I’m not sure if I’m doing this right, but it seems to me based on the math above the calculation would look something like this:
6×7 size: 56mm x 67mm therefore diagonal dimension is √(56^2 + 67^2) = 87.32mm
I assume then since we’re going the opposite direction, from a larger sensor down to a smaller, we’d divide 87.32 by 54.78, giving a crop factor of 1.59. Is this correct? Or am I doing this all wrong?
What is the right way to calculate the focal length change moving from a 6×7 lens to the GFX?
Nearly right. It would be 43.27mm/87.32mm = 0.4955
So basically it’s close enough to 0.5 that you could round up and use that.
The part you got wrong was “I assume then since we’re going the opposite direction, from a larger sensor down to a smaller”. Actually we’re going the same way as the GFX calculation. Since the GFX sensor is also much larger than full-frame. The 6×7 is just even larger!
I must not have been very clear, or I am misunderstanding you. Comparing the FOV in the GFX viewfinder vs. the viewfinder on the 6×7 camera it is clear that the focal length is effectively longer on the GFX than it is on the 6×7. The calculation above, in your original post, is for determining the effective focal length of a lens intended for a 35mm sensor on the larger GFX sensor. But what I’m after is the calculation for the effective focal length of a lens intended for a larger sensor, the 6×7, on the smaller GFX sensor. If I multiply the 43mm focal length by .4955 that would imply I should see a wider FOV on the GFX, rather than a narrower one. Since I am seeing a narrower FOV, I know that the crop factor must be greater than 1. Hopefully this makes my question clearer.
This seems to be what I was after:
https://www.dpreview.com/forums/thread/4305965#forum-post-61459143
So the 43mm Mamiya 7 lens on the GFX gives a FOV that would equal an approx. 70mm Mamiya 7 lens.
Ahhh! I see. Sorry, yes I totally misunderstood you there. I’m glad you got it figured out. This is a good topic for another post at some point 🙂 I’ll put it on my to-do list.
COMMENTJust multiply the focal length by .79. The 35mm sensor size is just a convenient reference to asses a familiar field of view, but focal length is not referencing a field of view (as opposed to angle of view), it is the distance from the lens nodal point to the sensor when focused at infinity. This is more apparent when using a bellows camera, as almost all non bellows lenses are telephoto: IE: they use lenses to simulate that lense to sensor distance at infinity. On a bellows camera an 80mmm lens would be 80mm from the film/sensor plane when focused at infinity – doesn’t matter what size that film/sensor plane is.
The short story – a 50mm is always a 50mm, but what is included in the angle of view will vary with sensor size. On the GFX – multiply the focal length of any lens by .79 and it will give you a sense of what you would see through a FF viewfinder.
I have the kitemaker. Though all the stories are well written I like the one called Time stops at Shamli
Thank you for this article, it saved me time writing down all the equivalents when deciding which lens to get for the wonderful GFX system.
you’re very welcome
So this conversation factor is not really correct.
You can’t go by diagonal dimensions when comparing the Fuji GFX system because it has another aspect ratio. You can get away with that with 1.6 and FF bodies because they are the same aspect ratio.
We measure field of view by width, not by height. So in actuality our crop factor is .82 instead of .79. Most any aspect ratio is going to crop the top and bottom since it’s pretty square as it is. Not the width. Unless you are shooting a square aspect ratio. But then you are framing from the height, and now technically it would be another conversion factor.
It’s being nit picky, but it is important to factor that in for your shooting. Because for me, I want to know my width since I like 2×3. So when I look at the 23mm f/4, I want to know how that compares to my 16-35mm. And if you want to get a good idea of the true focal length you will be using and you shoot FF or even 1.5/1.6 crop bodies. This will give you an accurate comparison and then you can amount for the extra height as you see fit.
The way I have done it is the standard that has been used for a while. There have always been other sensor aspects on the market, most notably M43 vs 35mm.
Your assumption is that field of view is measured by width. In a lot of cases that’s not true. Lens manufacturers, such as Sony and Canon, quote their view as a diagonal angle. To you, width might be more important. But for some people, it might be height. I think that is probably their logic in using the diagonal field of view in lens specifications. It satisfies both, and gives people a useful-enough constant by which to compare things.
You have done an excellent job of addressing the main topic of the article, explaining the concept of equivalent focal lengths, and how to calculate them. And, as you point out this works really well to tell you what field of view you will experience. I like an 85mm lens in full-frame for portraits, so if I was selecting a GFX lens to get the same angle of view (allowing me to use it at the same working distance in a studio, for instance) I would need to get the 110mm. This is all pretty basic, and the article is intended for a general audience who aren’t familiar with with all this, and you do a nice job explaining it.
Then, without any explanation you try to apply these same calculations to f/stops. And while I’m pretty sure I know what you mean, I think the claim that, for instance, the GF 80mm f/1.7 R WR has the equivalent f-stop to a f/1.3 on a full frame is mostly wrong, and extremely misleading, especially for less experienced photographers who are still having things like crop-factors explained to them.
Recall that the f-stop is *first and foremost* used to set exposure. That is for any given exposure increasing the size of the aperture increases the amount of light, such that adding one full stop of aperture can be compensated by decreasing one full stop of exposure time. Old light meters had these charts built into them. You would measure the light, and then you would have a set of aperture / shutter speed combinations that would result in a properly exposed pictures. If f/4 at 1/250th was correct, then using the reciprocating nature of the two values we know that if we open up the lens one full stop to f/2.8 (allowing more light in) to maintain the correct exposure we will cut the shutter speed by one full stop to 1/125th of a second.
The important thing about all this is that it is not sensor dependent. This is why if you look at old light meters, which were designed to be used with all the wildly different formats of film available in the pre-integrated light meter era of photography (roughly before 1955) their as no inputs or different outputs based on film size. The correct f/stop and shutter speed is the same, whether on a 4×5 view camera, medium format Rolleiflex 6 cm X 6 cm, or 35mm pre-war Leica rangefinder. (None of which has built in light meters, and of which could use the same handheld light meter).
To put simply: aperture measure (f-stop) is sensor-size independent in terms of the exposure triangle, its primary function.
You can easily prove this to yourself if you have and APS and Full Frame camera with the same mount (like Sony, Nikon and Canon all make). Pick a nice lens, preferably one with a built in tripod collar. Say a 300mm f/2.8. Do this in your well lit studio:
First: Attach the full frame camera. Shooting in manual mode, with ISO set to 100 do the following: Open the lens up all the way. Adjust the shutter speed to get the best exposure. Let’s say it turns out to be 1/500th of a second. Take the shot.
Second: Without moving the tripod or changing anything on the lens, remove the full-frame camera and replace it with the APS C camera. Set it to the exact same shutter speed and ISO. Leave the aperture the same. So, in our expample take another picture with ISO at 100, aperture all the way open at f/2.8 and shutter speed set to 1/500th of a second.
The result will be that both pictures will be exposed the same. What will be different is the image angle of view. The APS image will only contain the center of the the full frame image. It is as if you took the full-frame image and cut (cropped) it on all four sides.
But the exposure will be identical. The depth of field and bokeh will be identical too. Again, it will be just like you cropped the full-frame picture. If you print both pictures, the full image printed edge to edge on the same size paper the APS picture will appear to have more magnification. (Or “more zoom”). If you print both pictures so that the subject is the same size in them the APS picture will have empty space around all four edges.
The basic lens performance is not affected by the sensor size of the camera attached to it.
Thus is extremely misleading (especially for beginner photographers, such as this column is meant for).
What I think you meant to say was that “using this medium format lens at the distanced needed to achieve the same scene framing as you would with a 35mm with the same field of view (aka equivalent focal length) will result in depth of field similar to a 35mm lens with this aperture shot wide open”
OK, that’s true. But the primary function of f/stops is as a tool to adjust exposure and reciprocate time (shutter speed). It’s not called the “bokeh button” and, while that’s important, it’s not more important than the primary function of the f/stop.
In summary f/2 is f/2 in terms of exposure whether it’s on a 8×10 view camera or a cell phone. That’s why light meters are sensor independent.
Throwing that misleading information in, with no attempt to explain it is unfortunate. It’s a blemish on an otherwise fine article.
I think we have different opinions. “But the primary function of f/stops is as a tool to adjust exposure” Is it? It does do that, yes. But it also adjusts the depth of field. I think if you ask most photographers, they will probably tell you that they primarily think of f-stop as a mechanism to control DOF. I think this was different in the days of film where you would have to pick one film speed and load that into the camera. But in a digital era, where ISO can be used as an easy exposure adjustment, perhaps people’s ideas have changed?
F-stop is a mechanism to control DOF. Yes. But that is an irrelevant reply. Forget misapplying focal length formulae to aperture. It’s wrong. The same amount of light at the same f-stop hits the individual pixel, regardless of the sensor size.
Here’s a quote from B&H (NY).
“In photography, aperture is expressed as a ratio of the focal length to the diameter of the aperture opening. The ratio is commonly referred to as an f/number, f/stop, focal ratio, f/ratio, or relative aperture.
This ratio is based on physical measurements of the lens and is completely independent of the size of the camera’s sensor or the size of the film you are shooting.”
Your key statement is that you and the previous respondent are of different opinions. Er, I think you are confusing opinions with facts as so many do now. No, you are not entitled to your own facts. Please do not continue to promote this ridiculous error in your otherwise worthy site.
Footnote –
The only thing that could affect f-stop I suspect is if the lens vignetted badly and then was dropped onto a cropped sensor. The centre being brighter might push the actual averaged overall f-stop a fraction faster. But the effect would be opposite on an a medium format sensor.
But that’s a mere speculation on my part. And I’m happy to be corrected.