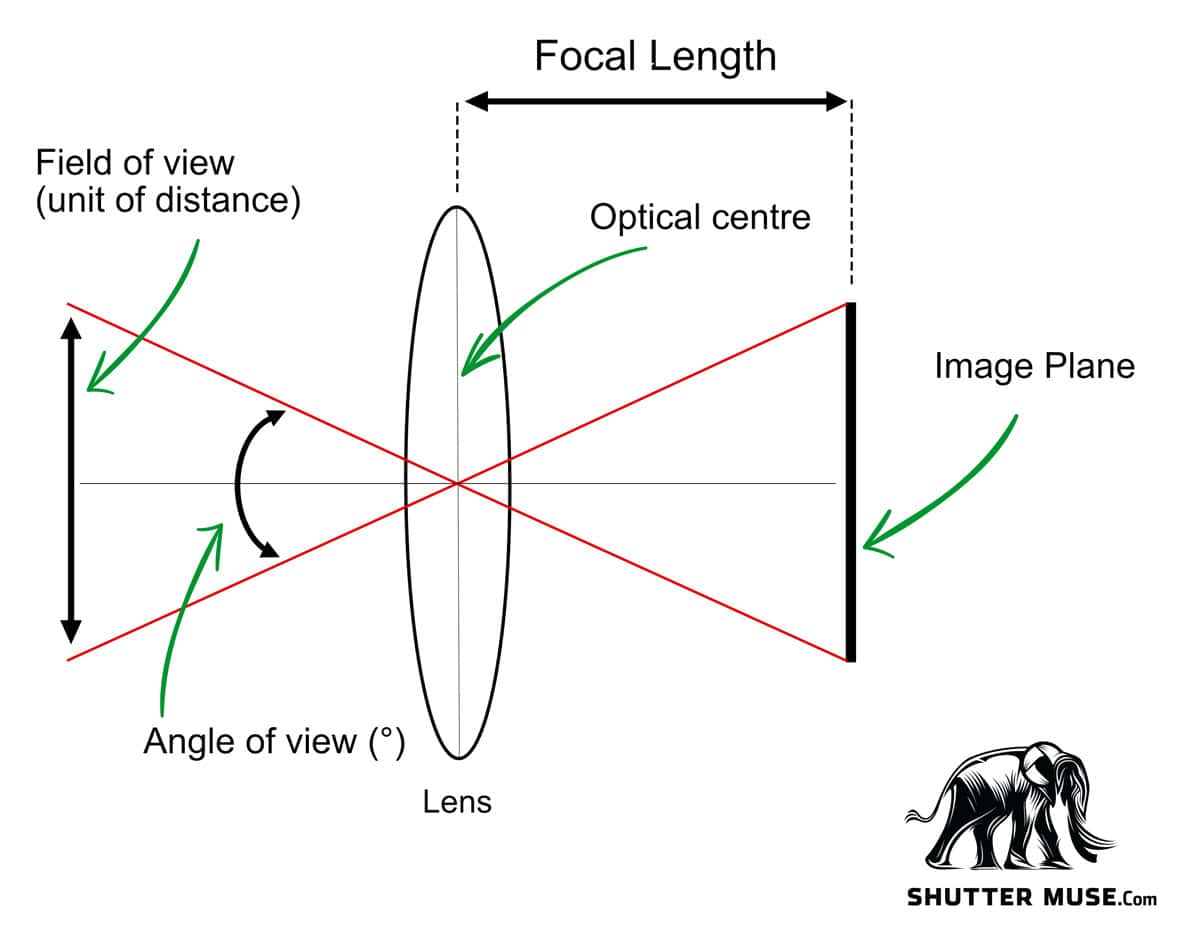
As I continue to build out the photographic knowledge base on the site with articles like Understanding Neutral Density Filter Names and Numbers, and Understanding Aperture, I thought I’d write a quick post about how to calculate field of view for a photographic lens. Lenses are usually described by their focal length, expressed in mm, but how does this translate to field of view?
If you read lens specifications (yes, I’m that kind of guy) on manufacturer’s websites, they’ll often quote the field of view (F.O.V) of a lens as well as the focal length. When they do this in photographic terms, they’re talking about horizontal field of view in degrees, and whilst any lens will also have both a vertical and a diagonal field of view, they are rarely talked about in relation to photographic lenses.
The larger the field of view, the wider the lens is and the more of a scene you are going to see with your camera. Telephoto and super telephoto lenses have very small fields of view, just a few degrees, so they aren’t able to see very much of the scene in front of them, although the compensating virtue is that what they do see, is much larger in the frame. A wide angle lens for landscape photography has a very small focal length, and therefore a large field of view that lets you record broad landscapes in a single shot.
Equation For Calculating Angle of View
Simple trigonometry will give us the equation:
Angle of view (in degrees) = 2 ArcTan( sensor width / (2 X focal length)) * (180/Ï€)
Note: If your calculator is working in radians, you need the (180/Ï€) part at the end. if your calculator is working in degrees, you do not need that bit! If you aren’t sure… it will become pretty obvious when you run the equation as results will be wildly wrong.
Equation for Calculating Linear Field of View
As well as calculating the angle of view, we can also use the same trigonometry to calculate the field of view as a linear measurement, as long as you know the distance to your subject, or, if you know the size of your subject and the focal length you are going to use, it could tell you how far away from it you need to be to get it to fill the frame. The units of measurement will be constant in the equation, so if you use metres as your distance to subject, the linear field of view will also be in metres.
Linear field of view = 2 (Tan (Angle of view/2) X Distance to Subject)
Common Focal Lengths and Their Corresponding FOVs
Since the equation for field of view contains the sensor width, which determines the crop factor of a sensor, this is another way to see the effect that the crop factor of a camera has on an image. The smaller the sensor, the larger the crop factor, and the smaller the field of view for a given focal length. Below I have included data for full frame field of view, as well as the three most common digital crop factors. If you want to learn more about crop factor, you can read my tutorial: How To Calculate a Camera’s Crop Factor.
If you want to use the field of view equation on this page to calculate the field of view for a sensor size other than the four that have been provided, you’ll need to refer to use this list of common sensor sizes and their crop factor.
Full frame 35mm (36mm sensor width)
| Focal Length | Field of VIew |
| 15mm (Fisheye) | 180.0 |
| 11mm | 117.1 |
| 14mm | 104.3 |
| 16mm | 96.7 |
| 24mm | 73.7 |
| 35mm | 54.4 |
| 50mm | 39.6 |
| 85mm | 23.9 |
| 100mm | 20.4 |
| 150mm | 13.7 |
| 200mm | 10.3 |
| 300mm | 6.9 |
| 400mm | 5.2 |
| 500mm | 4.1 |
| 600mm | 3.4 |
| 800mm | 2.6 |
| 1000mm | 2.1 |
| 1200mm | 1.7 |
Nikon DX APS-C (1.5x) (23.6mm sensor width)
| Focal length (35mm) | Equivalent focal length | Field of View |
| 11mm | 16.5 | 94.0 |
| 14mm | 21 | 80.3 |
| 16mm | 24 | 72.8 |
| 24mm | 36 | 52.4 |
| 35mm | 52.5 | 37.3 |
| 50mm | 75 | 26.6 |
| 85mm | 127.5 | 15.8 |
| 100mm | 150 | 13.5 |
| 150mm | 225 | 9.0 |
| 200mm | 300 | 6.8 |
| 300mm | 450 | 4.5 |
| 400mm | 600 | 3.4 |
| 500mm | 750 | 2.7 |
| 600mm | 900 | 2.3 |
| 800mm | 1200 | 1.7 |
| 1000mm | 1500 | 1.4 |
| 1200mm | 1800 | 1.1 |
Canon APS-C (1.6x) (22.5mm sensor width)
It must be noted here that Canon has actually used difference sensor sizes for their APS-C cameras over the years. Since the sensor dimension does affect the field of view, this should be taken into account in order to be 100% accurate. For the data table below I have chosen to use the sensor width of 22.5mm because this is the one that Canon seem to have stuck with for their own calculations, and it is also the dimension that gives exactly a 1.6x crop factor. Whilst they do have 22.3mm and 22.4mm sensor widths on the market as well, this minuscule difference would not actually make any noticeable difference to your images, but if you ran your own calculations for your own camera and found they did not match my numbers, this will be the cause of the difference. It was the source of some head scratching for me when I was figuring all this out myself!
| Focal length (35mm) | Equivalent focal length | Field of View |
| 11mm | 17.6 | 91.3 |
| 14mm | 22.4 | 77.6 |
| 16mm | 25.6 | 70.2 |
| 24mm | 38.4 | 50.2 |
| 35mm | 56 | 35.6 |
| 50mm | 80 | 25.4 |
| 85mm | 136 | 15.1 |
| 100mm | 160 | 12.8 |
| 150mm | 240 | 8.6 |
| 200mm | 320 | 6.4 |
| 300mm | 480 | 4.3 |
| 400mm | 640 | 3.2 |
| 500mm | 800 | 2.6 |
| 600mm | 960 | 2.1 |
| 800mm | 1280 | 1.6 |
| 1000mm | 1600 | 1.3 |
| 1200mm | 1920 | 1.1 |
Micro Four Thirds (2x) (22.3mm sensor width)
| Focal length (35mm) | Equivalent focal length | Field of View |
| 11mm | 22 | 78.6 |
| 14mm | 28 | 65.5 |
| 16mm | 32 | 58.7 |
| 24mm | 48 | 41.1 |
| 35mm | 70 | 28.8 |
| 50mm | 100 | 20.4 |
| 85mm | 170 | 12.1 |
| 100mm | 200 | 10.3 |
| 150mm | 300 | 6.9 |
| 200mm | 400 | 5.2 |
| 300mm | 600 | 3.4 |
| 400mm | 800 | 2.6 |
| 500mm | 1000 | 2.1 |
| 600mm | 1200 | 1.7 |
| 800mm | 1600 | 1.3 |
| 1000mm | 2000 | 1.0 |
| 1200mm | 2400 | 0.9 |
Thanx for the math. Can the view angle and/ or field of view for fish-eye lenses both rectilinear and circular image types also be calculated? It is my understanding the formulas are more complicated.
I am interested because I have two fisheye Zuiko lenses from OM-2 & 4 cameras which I would like to use with adapter on Panasonic G 85 or Canon M 50. Can you help? TIA
I would imagine that is more complicated but I’m afraid I’m not sure.
Field of View. How many feet both horizontally and vertically in FOV using a 2000mm lens at 800 yards? I am trying to decide if I want to spend the money on a Nikon that comes with that lens.
I’ll be honest Michael, I don’t have time to do the math for you. The idea was to create a resource for people to calculate this themselves. All the equations you need are right here on the page. Just plug your numbers in 🙂
your FOV table is wrong. i think you took 36mm width instead of the diagonal.
=2*ARCTAN(SQRT(24^2+36^2)/(2*”focallength”))*(180/PI())
As far as I can tell, it is correct. I just plugged some values into other online FOV calculators and the FOV calculator in the most popular photography iPhone app and all got the same answers that are in my table. 36mm is the width of a full frame sensor.
Dan, I’m a newbie to landscapes, and I’m not a professional. So, here’s a little feedback. Please understand that I don’t necessarily have the right language to ask the right questions. What I was really looking for is a way to know what general lens size to use to get a “how large a field of view. The math is helpful, but really not intuitive, especially if your last experience with higher math was 30+ years ago. What was a very useful visual for demonstrating angle of view is the first illustration you had, namely, the “topdown” view of the camera with cones coming forward in different colors. A visual chart or series of charts showing an object at say 200 yards, with the focal point in the center, and a second overlay on top of that showing how much distance to the front & back of the focal point remains in focus relative to the aperture would be ideal. I realize you are probably laughing out loud at this, & don’t have anywhere near enough time for a project of that size, & probably even less inclination to actually do it, but it would be enormously helpful, and a lot more visually intuitive. Thanks so much.
Thanks for the suggestion Kay. I like the idea, but there are many phone apps out there that offer this already, and they do a better job than I could ever do. I would suggest buying the app called “PhotoPills”, it has angle of view and depth of field calculators in it and it’s a great app for many things related to photography.
I need to shoot down on a square card table, 35 inches on each side (including margins) at a distance of about 1 meter. I am using a Panasonic G6 with the 14-42mm kit lens set at 14mm. Online calculators using the formula FOV (rectilinear) = 2 * arctan (frame size/(focal length * 2) indicate that the 14mm focal length should cover 35.14 inches in the vertical dimension at a distance of 41 inches. When I actually tried it, I had to be at least 11 feet back from the table. What gives?
I would check that your camera is in full output. If you use are using a smaller output resolution, your FoV will be cropped. The frame size input will be smaller.
Note that this equation HSize/2=f*Tan(FoV/2) is inaccurate if your DSLR lens has >1% distortion. So, it shouldn’t be used for lenses like the Canon 11mm-22mm and most <15mm EFL 35mm-format type lenses. The G6 14mm has ~5% distortion.
The equation with distortion is quite a bit more complicated, so even apps like PhotoPills haven't modelled it. It has 4 variable coefficients and an additional SIN function. Here is a calculator which extends to lenses with distortion:
https://commonlands.com/pages/fov-calculator
Thanks Max! Interesting stuff. Thanks for the link.
How about a compact camera such as Olympus tg4 and tg5