I recently received a comment on my popular article – The Ultimate Guide to Extension Tubes – which asked how you would go about calculating the new MFD (minimum focus distance) of a lens, once you have added an extension tube. In that original post I did include the mathematics for calculating the new maximum magnification of a lens with an extension tube, but at the time I decided not to dig deeper and explore the calculation of the new MFD itself, since the math is a little longer. The new comment reminded me about it, so I decided to write this new post to explore it and do an example and a test based around real world lens measurements.
By this point I probably don’t need to tell you this but: Nerdy optical math stuff is coming! Some of you love it, some of you don’t 😉 You have been warned.
The Thin Lens Equation
d0 = object distance from lens
di = image distance from lens
f = focal length of lens
Important Note About Accuracy
If you really want to know exactly what your new MFD is, the best way is still to put the extension tube on the lens and move an object closer to the camera until it can no longer focus, them simply measure that distance. MFD is measured to the focal plane of the camera (sensor) and not the front of the lens.
Of course this means that you already need to own the extension tube, and I can see a reason why people would want this information prior to making the purchase. Most likely, you would be trying to decide whether to buy a 12mm extension, or a 25mm extension if you already had a pretty good idea about the kind of subjects you want to photograph, and how close you might be able to get to them.
The problem is that all lenses are designed very differently, and all the mathematics behind these things has to rely on the thin lens equation. This equation has to assume that a lens is comprised of a single element, and also that the lens element itself is “thin”, in other words the distance that light travels through the lens isn’t taken into account, and neither are optical effects due to the thickness. In photographic lenses neither of these assumptions are true, so the only answers we can come up with are simply best guesses. It also can’t take into account the fact that lens elements shift within a lens as you focus it, so you’re basically working with an unknown moving target. The only way to get truly perfect results would be by physical experimentation as I described in the first paragraph of this sub-section. As long as you keep that in mind though, we can still get some useful results. What I’m going to do here is demonstrate the theoretical change in MFD of a lens using an extension tube, and then I’ll measure it physically with my own copies of the lens so that we can examine how much the theoretical results might differ from the real world MFD.
Revisiting Magnification Change with Extension Tubes
This was covered in the aforementioned extension tube guide, but for those that haven’t read that one, it’s important to get the whole picture, so we’ll start here.
You’ll need to start with with magnification of your lens, which can be found in the lens specifications that are listed on the manufacturers website.
New magnification = Native lens magnification + (extension amount/focal length)
Example 1: The Canon 40mm f/2.8 STM pancake lens has a native magnification of 0.18x. If we use a 12mm extension tube on it, our new magnification will be 0.18 + (12/40) = 0.48x
Example 2: Using the same Canon 40mm lens with stacked 12mm and 25mm extension tubes would give us a magnification of 0.18 + ((12+25)/40) = 1.11x
The formula for new magnification is also linked to the thin lens formula. A lens’ magnification is generally written as M = (hi/ho) = -(di/do), where M = magnification, hi = image height, ho = object height, and do and di are the already defined parts of the thin lens formula, distance to object and distance to image. If you haven’t taken a second to think about it before, magnification is simply the ratio of an object’s height in real life, compared to the height of that object’s projection onto the camera’s sensor, or (hi/ho).
If you did the trigonometry on the triangles in the diagram, you’d see that much of it cancels out and reveals that (hi/ho) is also equal to -(di/do). The negative value comes from the image being flipped upside down, but essentially this can be ignored in real life since sensors are installed upside down in the camera to overcome this.
How to Calculate Change in MFD
Now we have two equations, the thin lens equation and the magnification equation, that have some common terms in them. We also need to remember that when a lens is focussed at its absolute minimum focus distance, MFD = di + do which hopefully should be clear from the diagram, and what was mentioned earlier about MFD being the distance to the camera’s sensor and NOT the distance to the front of the lens.
This actually gives us everything we need to calculate the new MFD of a lens that is using an extension tube, so let’s take a look at an example.
Example – Canon 50mm f/1.8 STM with 25mm extension tube
Known data points:
- Native lens magnification M = 0.21 (from manufacturer specs)
- MFD: 350mm (from manufacturer specs)
Using our previous formula for change in magnification, we can calculate that the new magnification of the 50mm lens + 25mm extension tube is (0.21 + (25/50)) = 0.71. This is the first stepping stone to figuring out the new MFD of this lens+extension tube combination.
The thin lens formula tells us that 1/f = 1/di + 1/do so we know that 1/50 = 1/di + 1/do
From the magnification formula we also know that di / do = M and this means that 0.71 = di / do
We need to find both di and do so that we can add them together to get our new MFD.
Since we can’t solve for both di and do simultaneously we can use the fact that 0.71 = di / do and hence di = 0.71 x do. With this we can eliminate di from the equation to give us: 1/50 = 1/(0.71 x do) + 1/do.
Now all we have to do is solve for do.
First we will multiply both sides by do to get: (1/50) do = (1/0.71) + 1 => (1/50) do = 2.408
Then we can multiply both sides by 50 to leave us with the simple equation: do = 50 + (50/0.71) => 120.423mm
Now that we have a value for do we can plug it back into our original equation of 0.71 = di / do => di = (0.71 x 120.423) => 85.50mm
We did it!
di = 85.5mm
do = 120.423mm
MFD = (85.5 + 120.423) = 205.923mm
So the Canon 50mm f/1.8 STM lens has a native MFD of 350mm, but if you add a 25mm extension tube to it then you’ll be (theoretically) able to focus down as close as 206mm. That’s a pretty big improvement!
Change in MFD Equation
I wanted to include the above example from the beginning so that we can see how we got to the answer, but the whole process can also be represented with the following equations:
do = f + (f / (m + (e/f)))
di = do (m + (e/f))
New MFD = di + do
Where f = focal length, e=extension tube length, m=native lens magnification without the extension tube and di and do are distance to image and distance to object as we have become familiar with already. If you have an easier way to simplify this, I’m all ears, just leave a comment at the bottom of the page.
Real World Testing
As I mentioned earlier in the post, this math has to make some pretty big assumptions so it’s not going to give us a perfectly accurate result, but how far off are we? I own a 25mm extension tube at the Canon 50mm STM lens, and in my physical testing I was able to focus down to 204mm which is only a 1% variation from the theoretical value. I was expecting it to be more than that, but this is likely down to the relative simplicity of the “nifty fifty” lens. I expected more complex lens designs with more elements in them, such as a 24-70 f/2.8 to exhibit more of a difference.
The Canon 24-70 f/2.8 L II has an MFD of 380mm and a native magnification of 0.21. With a 25mm extension tube, this magnification would become 0.57, and if we plug all that into the previous math that we did, we get a new MFD of 303mm for this lens with the extension tube. In real world testing though, I was able to focus the 24-70 f/2.8 L II down to 237mm with the 25mm extension tube. That’s a pretty dramatic 28% variation from the theoretical value, so you definitely need to be careful when making assumptions with complex zoom lens designs.
Corrections?
I’m fairly sure of the mathematics in this article, but with complex subjects like this there’s always the possibility for a small mistake. If you spot something that isn’t quite right, please leave a comment below. If you do your own real world testing of an extender/lens combination, please also leave the data in a comment!

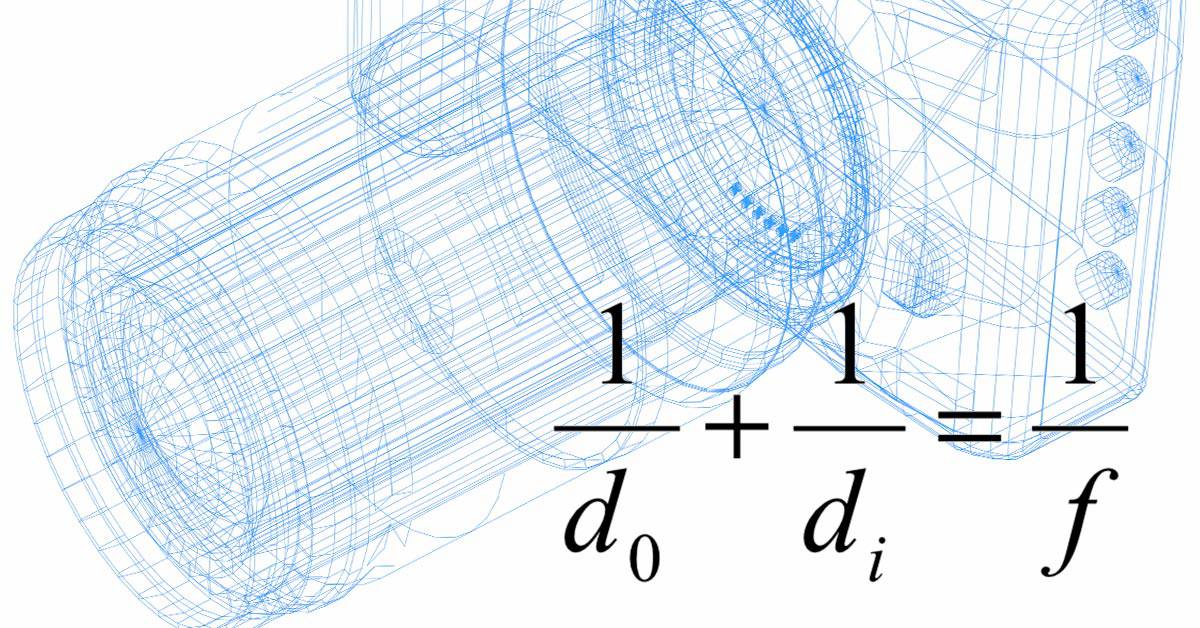
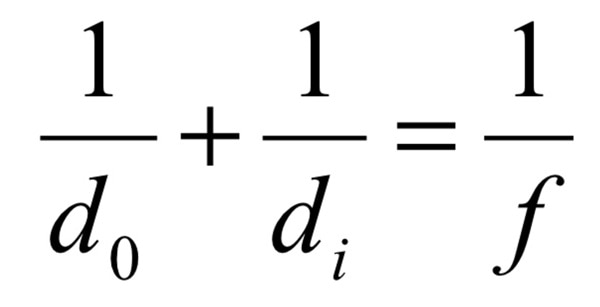







Hi Dan,
Thanks for the information!
Your example 2 should perhaps be revised thus: 0.18 + ((12+25)/40) = 0.92x
Example 2: Using the same Canon 40mm lens with stacked 12mm and 25mm extension tubes would give us a magnification of 0.18 + ((12+25)/50) = 0.92x
Aha! I knew there were far too many numbers on this page for me to have not messed one of them up. Thanks for spotting the error.
Hi Dan,
This is very helpful. But I think you made a mistake in the general formula. I arrived this formula for di:
di = do (m + e/f)
Using your formula for di would not arrive to 85.5 mm
Thanks,
Yep you’re right. My mistake. Thanks for figuring it out. Not sure how I got 9/10ths of the way through that and screwed it up at the last minute!
I have tried with Canon 60mm MFD = 200 and magnification = 1 and whatever formula is used the MFD with extension tube is always longer than without it….
Sorry about that, I fell at the last hurdle and there was an error in the equation for di. It has been fixed.
I agree with Namur’s comment. I plugged in the Canon 400mm with 0.12x maximum magnification, and the result with 68mm of extension (3 stacked tubes) was MFD = 16.2′, yet the manufacture sped for MFD (no tubes) is 11.48′
If instead I use Jared’s equation for di, the new MFD (with stacked tubes) is 7.5′, It appears to be correct.
Sorry about that. Somehow I got it all right until the last hurdle. I have edited the article to correct the di formula.
Dan, with telephoto lenses or zooms where the focal length is longer than the physical length of the lens, the virtual location of the thin lens may be in fact be some distance in front of the lens. Possibly solving for the location of the virtual thin lens and using that to calculate virtual MFD’s before and after adding the tube will give less error. Then correct the “after” virtual MFD to a real MFD. I ran into this problem trying to characterize the actual focal length of some surplus “mystery” projector lenses that used telephoto design in their optics. Having said this, even for a non telephoto lens, there may be some benefit of taking the same approach as the location of the “thin lens” is somewhere inside of the body of the lens.
“Possibly solving for the location of the virtual thin lens and using that to calculate virtual MFD’s before and after adding the tube will give less error”
Yeah you’re absolutely right. But the thin lens equation is, in itself an approximation because the whole thing assumes a single lens element which of course it isn’t. So whilst there are ways to make it more accurate… it’s beyond me 🙂
Dan, for what it’s worth, using a modification of your equations we can also evaluate MFD directly in terms of m, e, and f without the intermediate distances. Here, m is the lens maximum magnification, e is the extension tube length in mm, and f is the lens focal length in mm. Set
me = m + e/f
and
MFD = f*(1 + me)*(1+me)/me
With m = 0.21, e = 25mm, and f = 50mm we get
me = 0.21+ 25mm/50mm = 0.71
and
MFD = 50mm*1.71*1.71/0.71 = 206mm
I have a Canon EOS R camera and EOS RF f=35mm lens with m=0.5. I will be getting some free extension tubes up to 58mm. Will that much extension work with this lens? I don’t think so.
me = 0.5 + 58mm/35mm = 2.157
MFD = 35mm*3.157*3.157/2.157 = 162mm
If this number is correct, and it may be off as you showed in an example, then I don’t think this amount of extension will work. When the lens is focused for maximum magnification, the measured distance from sensor plane to the end of the lens is about 101mm. Inserting 58mm of extension tube increases this distance to 159mm. If MFD = 162mm, this leaves only 3mm working distance, which is the clearance between lens and subject. Even if this distance were feasible, the lens would likely block too much light from the subject. A potential solution would forego some magnification by removing extension or by backing away. It will be interesting to see which option is better.
Where are you getting RF extension tubes? I wasn’t aware of anyone making them yet?
As has already been stated, the thin lens equation makes a lot of assumptions. The biggest assumption is that the front principal plane and rear principal plane coincide. In real world lenses, there will be a separation distance between your principal planes. This separation distance may be positive or negative. From my own experience of measuring the cardinal points of photography lenses, I have found that the principal plane separation distance changes with the focus of the lens. I hope this helps to explain some of the error that you found in your experiment.
Thanks for your insight, Ric! That sounds like a contributing factor.
A question: Are there any iOS apps that will do the calculations? Could be super compelling.
Thanks for your wonderful write up. I learned a lot.